论文概况
Link: 360ProbDASH: Improving QoE of 360 Video Streaming Using Tile-based HTTP Adaptive Streaming
Level: ACM MM 17
Keyword:
Pre-fetch tiles, QoE-driven optimization, Probabilistic model, Rate and Viewport adaptation
工作范围与目标
应用层->基于 tile->viewport 预测的可能性模型+预期质量的最大化
针对小 buffer 提出了
target-buffer-based rate control算法来避免重缓冲事件(避免卡顿)提出 viewport 预测的可能性模型计算 tile 被看到的可能性(避免边缘效应)
形式化 QoE-driven 优化问题:
在传输率受限的情况下最小化 viewport 内的质量失真和空间质量变化(获取受限状态下最好的视频质量)
问题建模
形式化参数
$M*N$个 tile,M 指 tile 序列的序号,N 指不同的码率等级
$r_{i, j}$指比特率,$d_{i, j}$指失真,$p_{i}$指被看到的可能性($\sum_{i=1}^{N}p_{i} = 1$)
$\Phi(X)$指质量失真,$\Psi(X)$指质量变化
目标
找到推流段的集合:$X = {x_{i, j}}$,其中${x_{i, j}} = 1$指被第$<i, j>$个 tile 被选中;$x_{i, j} = 0$则是未选中。
$$ \underset{X}{min}\ \Phi(X) + \eta \cdot \Psi(X) \ s.t. \sum_{i=1}^{N}\sum_{j=1}^{M}x_{i, j}\cdot r_{i, j} \le R, \ \sum_{j=1}^{M}x_{i, j} \le 1, x_{i, j} \in {0, 1}, \forall i. $$
整个公式即为前所述的问题的形式化表达的公式化结果。
模型细节
$\Phi(X)$和$\Psi(X)$的计算=>通过考虑球面到平面的映射
通过计算球面上点的 Mean Squared Error 来得到 S-PSNR 进而评估质量:$d_{i, j}$来表示第${<i, j>}$个段的 MSE
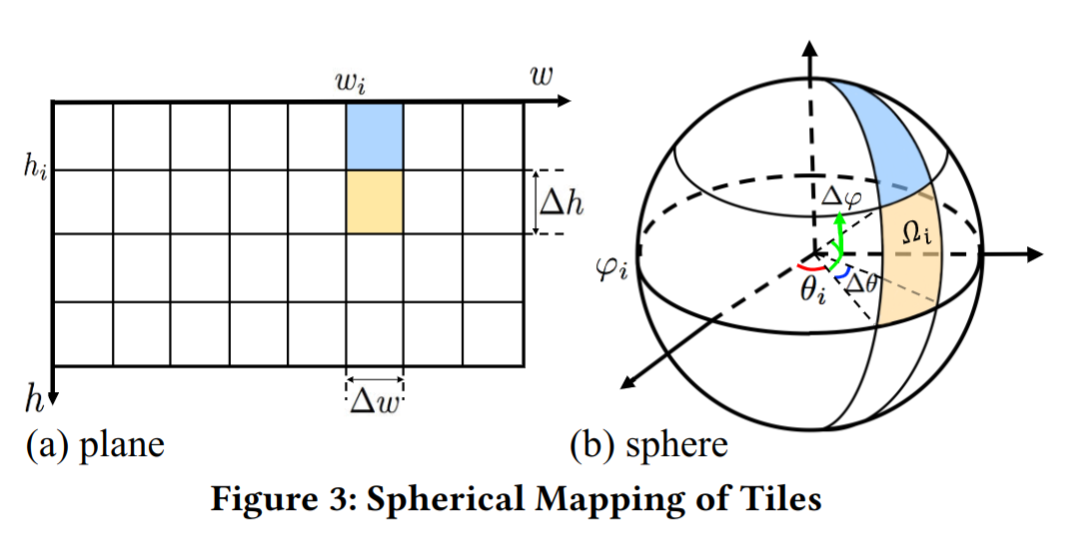
$$ \phi_i = \frac{\pi}{2} - h_i \cdot \frac{\pi}{H}, \Delta\phi = \Delta h \cdot \frac{\pi}{H}, \ \theta_i = w_i \cdot \frac{2\pi}{W}, \ \Delta\theta = \Delta w \cdot \frac{2\pi}{W}, $$
$H$和$W$分别指按照 ERP 格式投影之后的视频高度和宽度
第$i$个 tile 的空间面积用$s_i$表示:
$$ s_i\ =\ \iint_{\Omega_i}Rd\phi Rcos\phi d\theta \ =\Delta\theta R^2[sin(\phi_i + \Delta\phi) - sin\phi_i], $$
$R$指球的半径($R = W/2\pi$),所以整体的球面质量失真$D_{i, j}$可以计算出来:
$$ D_{i, j} = d_{i, j} \cdot s_i, $$
结合每个 tile 被看到的概率$p_i$可以得出$\Phi(X)$和$\Psi(X)$
$$ \Phi(X)=\frac{\sum_{i=1}^N\sum_{j=1}^MD_{i, j}\cdot x_{i,j}\cdot p_i}{\sum_{i=1}^N\sum_{j=1}^Mx_{i,j}\cdot s_i},\ \Psi(X) = \frac{\sum_{i=1}^N\sum_{j=1}^Mx_{i, j}\cdot p_i \cdot\ (D_{i,j}-s_{i} \cdot \Phi(X))^2}{\sum_{i=1}^N\sum_{j=1}^Mx_{i,j}\cdot s_i}. $$
Viewport 的可能性模型
方向预测=>线性回归模型
将用户的欧拉角看作是$yaw(\alpha)$,$pitch(\beta)$和$rool(\gamma)$,应用线性回归做预测
$$ \begin{cases} \hat{\alpha}(t_0 + \delta) = m_{\alpha}\delta+\alpha(t_0),\ \hat{\beta}(t_0 + \delta) = m_{\beta}\delta+\beta(t_0),\ \hat{\gamma}(t_0 + \delta) = m_{\gamma}\delta+\gamma(t_0). \end{cases} $$
预测错误的分布=>高斯分布,根据公式均值和标准差都能从统计信息中计算出来
收集 5 名志愿者的头部移动轨迹并投影到 3 个方向上绘制成图,实验结果为预测错误呈现高斯分布(样本数可能不够?)
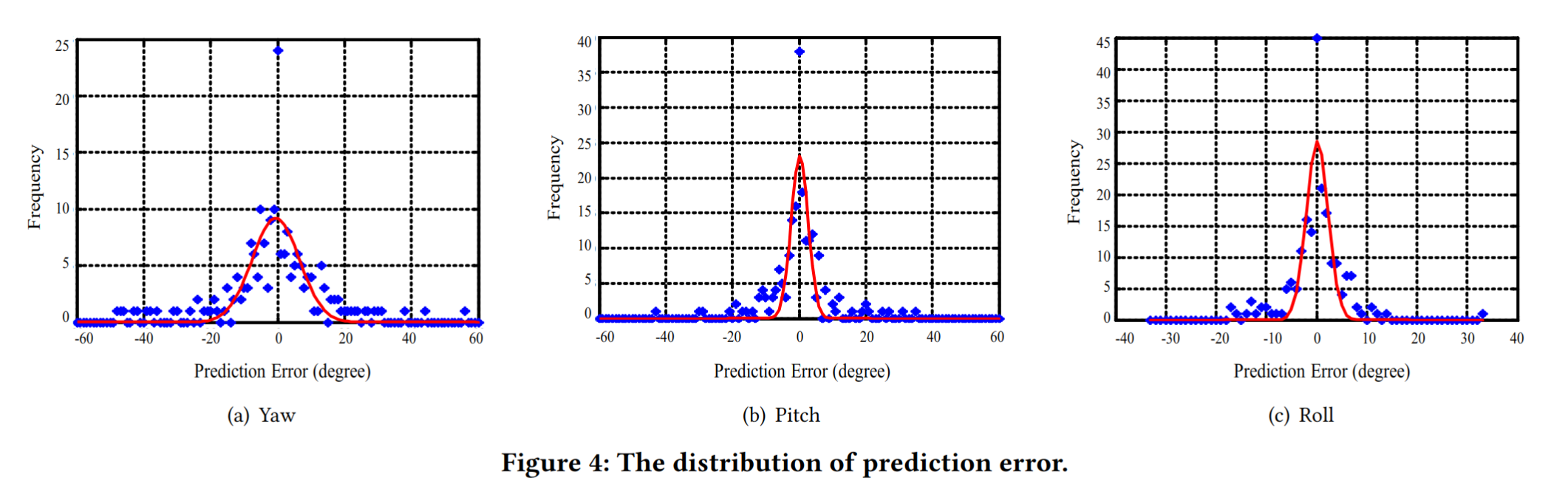
$$ \begin{cases} P_{yaw}(\alpha) = \frac{1}{\sigma_{\alpha}\sqrt{2\pi}}exp{-\frac{[\alpha-(\hat{\alpha}+\mu_{\alpha})]^2}{2\sigma_{\alpha}^2}},\ P_{pitch}(\beta) = \frac{1}{\sigma_{\beta}\sqrt{2\pi}}exp{-\frac{[\beta-(\hat{\beta}+\mu_{\beta})]^2}{2\sigma_{\beta}^2}},\ P_{roll}(\gamma) = \frac{1}{\sigma_{\gamma}\sqrt{2\pi}}exp{-\frac{[\gamma-(\hat{\gamma}+\mu_{\gamma})]^2}{2\sigma_{\gamma}^2}}. \end{cases} $$
3 个方向各自独立,因此最终的预测错误$P_E(\alpha,\beta,\gamma)$可以表示为:
$$ P_E(\alpha, \beta, \gamma) = P_{yaw}(\alpha)P_{pitch}(\beta)P_{roll}(\gamma). $$
球面上点被看到的可能性
球面坐标为$(\phi, \theta)$点的可能性表示为$P_s(\phi, \theta)$
因为一个点可能在多个不同的 viewport 里面,所以定义按照用户方向从点$(\phi, \theta)$出发能看到的点集$L(\phi, theta)$
因此空间点$s$被看到的可能性可以表示为:
$$ P_s(\phi, \theta) = \frac{1}{|L(\phi, \theta)|}\sum_{(\alpha, \beta, \gamma) \in L(\phi, \theta)}P_E(\alpha, \beta, \gamma), $$
球面上 tile 被看到的可能性
tile 内各个点被看到的可能性的均值即为 tile 被看到的可能性(可否使用其他方式?)
$$ p_i = \frac{1}{|U_i|} \sum_{(\phi, \theta) \in U_i} P_s(\phi, \theta). $$
$U_i$表示 tile 内的空间点集
Target-Buffer-basedRate Control因为长期的头部移动预测会产生较高的预测错误,所以不能采用大缓冲区(没有 cite 来证明这一点)
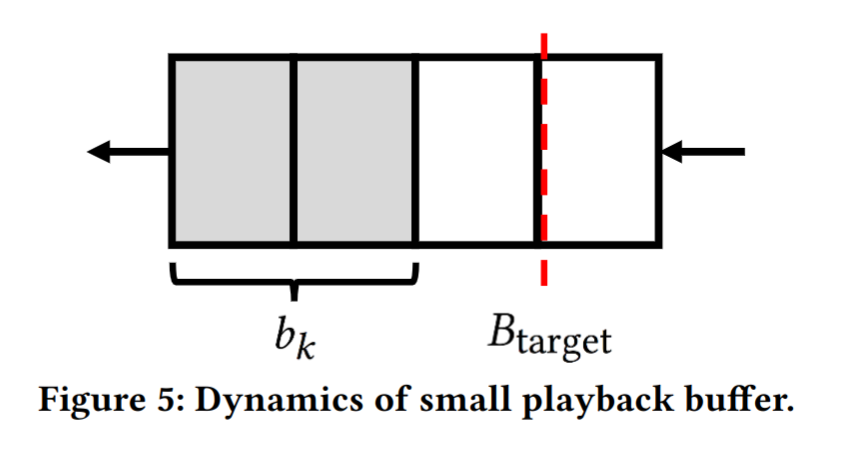
将处于相同时刻的段集合成一个块存储在缓冲区中。
在自适应的第 k 步,定义$d_k$作为此时的 buffer 占用情况(等到第 k 个块被下载完毕)
$$ b_k = b_{k-1} - \frac{R_k \cdot T}{C_k} + T $$
$C_k$表示平均带宽,$R_k$表示总计的码率
为了避免重新缓冲设定目标 buffer 占用$B_{target}$,并使 buffer 占用保持在$B_{target}$($b_k = B_{target}$)
因此总计的码率需要满足:
$$ R_k = \frac{C_k}{T} \cdot (b_{k-1} - B_{target} + T), $$
这里的$C_k$表示可以从历史的段下载信息中估计出来的带宽
设定$R$的下界$R_{min}$之后(没有说明为何需要设定下界),公式 12 可以修正为如下:
$$ R_k = max{\frac{C_k}{T} \cdot (b_{k-1} - B_{target} + T), R_{min}}. $$
实现
服务端
视频裁剪器
将视频帧切割成 tile
编码器
对 tile 进行划分并将其编码成多种码率的段
MPD 产生器
添加SRD 特性来表示段之间的空间关系
添加经度和纬度属性来表示
添加质量失真和尺寸属性
Apache HTTP 服务器
存储视频段和 mpd 文件,向客户端推流
客户端
基础:dash.js
额外的模块
QoE-driver Optimizer$$ Output = HTTP\ GET请求中的最优段 $$
$$ Input = Output\ of
\begin{cases} Target\ buffer\ based\ Rate\ Controller\ Viewport\ Probabilistic\ Model\ QR\ Map \end{cases} $$Target-buffer-based Rate Controller$$ Output = 总计的传输码率,按照公式13计算而来 $$
$$ Input = Output\ of\ {Bandwidth\ Estimation\ module $$
Viewport Probabilistic Model$$ Output = 每个tile被看到的可能性,按照公式10计算而来 $$
$$ Input = Output\ of
\begin{cases} Orientation\ Prediction\ module\ SRD\ information \end{cases} $$QR MapQR=>Quality-Rate$$ Output = 所有段的QR映射 $$
$$ Input = MPD中的属性 $$
Bandwidth Estimation(没有展开研究,因为不是关键?)$$ Output = 前3秒带宽估计的平均值 $$
$$ Input = 下载段过程中的吞吐量变化 $$
可以通过
onProgess()的回调函数XMLHttpRequest API获取Orientation Prediction$$ Output = 用户方向信息的预测结果(yaw, pitch, roll) $$
$$ Input = Web\ API中获取的DeviceOrientation信息,使用线性回归做预测 $$
评估
整体设定
- 将用户头部移动轨迹编码进播放器来模拟用户头部移动
- 积极操控网络状况来观察不同方案对网络波动的反应
详细设定
服务端
视频选择
2880x1440 分辨率、时长 3 分钟、投影格式 ERP
切分设置
每个块长 1s($T=1$)、每个块被分成 6x12 个 tile($N=72$)
每个段的码率设置为${20, 50, 100, 200, 300}$,单位 kpbs
视频编码
视频分包
注意事项
每个段的确切尺寸可能与其码率不同,尤其对于长度较短的块。
为了避免这影响到码率自适应,将段的确切尺寸也写入 MPD 文件中
客户端
缓冲区设定(经过实验得出的参数)
$B_{max}=3s$,$B_{target}=2.5s$,$R_{min}=200kbps$,$权重\eta=0.0015$
高斯分布设定
Yaw Pitch Roll $\mu_{\alpha}=-0.54,\ \sigma_{\alpha}=7.03$ $\mu_{\beta}=0.18,\ \sigma_{\beta}=2.55$ $\mu_{\gamma}=2.16,\ \sigma_{\gamma}=0.15$
比较对象
- ERP:原始视频格式
- Tile:只请求用户当前 viewport 的 tile,不使用 viewport 预测,作为 baseline
- Tile-LR:使用线性回归做预测,每个 tile 的码率被平均分配
性能指标
- 卡顿率:卡顿时间占播放总时长的比例
- Viewport PSNR:直接反应 Viewport 内的视频质量
- 空间质量差异:Viewport 内质量的协方差
- Viewport 偏差:空白区域在 Viewport 中的比例