论文概况
Link:360SRL: A Sequential Reinforcement Learning Approach for ABR Tile-Based 360 Video Streaming
Level:ICME 2019
Keywords:ABR、RL、Sequential decision
创新点
- 在 MDP 中,将 N 维决策空间内的一次决策转换为 1 维空间内的 N 次级联顺序决策处理来降低复杂度。
问题定义
原始的全景视频被划分成每段固定长度为 $T$ 的片段,
每个片段包含 $N$ 个分块,并以 $M$ 的码率等级独立编码,
因此对每个片段,有 $N \times M$ 种可选的编码块。
为了保证播放时的流畅性,需要确定最优的预取集合:
${a0, …, a_i, …, a{N-1}}, i \in \lbrace 0, …, N-1 \rbrace, a_i \in \lbrace 0, …, M-1 \rbrace $
分别用 $q_{i, a_i}$ 和 $w_{i, a_i}$ 表示码率选择为 $a^{th}_i$ 的 $i^{th}$ 分块的质量和相应的分块片段大小。
用 $p_i \in [0, 1]$ 表示 $i^{th}$ 块的被看到的可能性。
顺序 ABR 决策
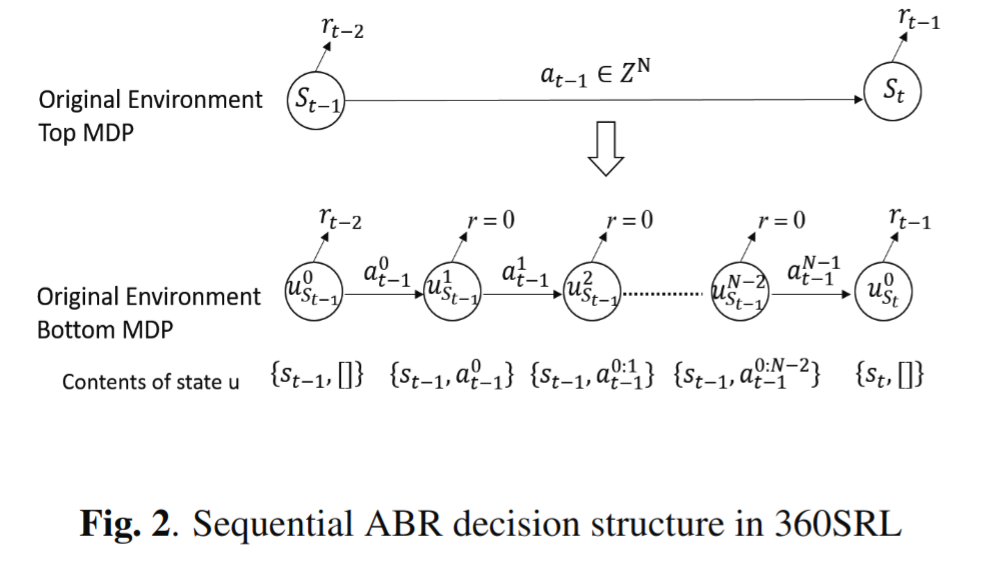
代理设计
状态
对于 $i^{th}$ 维,输入状态包括原始的环境状态 $s_t$ ;
与之前维度的动作集合相关的信号: $u^{i}_{s_t} = \lbrace Th, C_i, p_{0:i-1}, q_{0:i-1}, b_t, p_i, S_i, Q_{t-1} \rbrace$
$Th$ :表示过去 m 次下载一个段的平均吞吐量;
$C_i \in R^M$ :表示 $i^{th}$ 个分块的可用块大小向量;
$p_{0:i-1}$ 和 $q_{0:i-1, a^{0:i-1}_{t}}$ 分别表示选中的码率集合和看到之前 $i-1$ 个分块的概率集;
$b_t$ 是缓冲区大小;
$p_i$ 是 $i^{th}$ 个分块被看到的可能性;
$S_i$ 是之前选择的 $i-1$ 个分块的块大小之和: $S_i = \sum^{i-1}_{h=0} C_{h, a^h_t}$ ;
$Q_{t-1}$ 记录了最后一个段中 $N$ 个分块的平均视频质量;
动作
动作空间离散,代理输出定义为价值函数:$f(u^i_{s_t}, a^i_t)$
表示所选状态的价值 $a^i_t \in \lbrace 0, …, M-1 \rbrace$ 处于状态 $u_{s_t}^i$ .
回报
回报定义为下列因素的加权和:
平均视频质量 $q^{avg}_t$,空间视频质量方差 $q^{s_v}_t$,时间视频质量方差 $q^{t_v}_t$ ,重缓冲时间 $T^r_t$
$$ q^{avg}_t = \frac{1}{\sum^{N-1}_{i=0} p_i} \cdot \sum^{N-1}_{i=0} p_i \cdot q_{i, a_i} $$
$$ q^{s_v}_t = \frac{1}{\sum^{N-1}_{i=0} p_i} \cdot \sum^{N-1}_{i=0} p_i \cdot |q_{i, a_i} - q^{avg}_t| $$
$$ q^{t_v}_t = |q^{avg}_{t-1} - q^{avg}_t| $$
$$ T^r_t = max \lbrace T_t - b_{t-1}, 0 \rbrace $$
$$ R_t = w_1 \cdot q^{avg}_t - w_2 \cdot q^{s_v}_t - w_3 \cdot q^{t_v}_t - w_4 \cdot T^r_t $$
训练方法
使用DQN作为基本的算法来学习动作-价值函数 $Q(s_t, a_t; \theta)$ ,其中 $\theta$ 作为参数,对应的贪心策略为 $\pi(s_t; \theta) = \underset{\theta}{argmax} Q(s_t, a_t; \theta)$ 。
DQN网络的关键想法是更新最小化损失函数的方向上的参数:
$$ L(\theta) = E[y_t - Q(s_t, a_t; \theta)] $$
$$ y_t = r(s_t, a_t) + \gamma Q(s_{t+1}, \pi(s_{t+1}; {\theta}’); {\theta}’) $$
${\theta}’$ 表示固定且分离的目标网络的参数;
$r(\cdot)$ 是即时奖励函数,即上面公式 5 中的 $R_t$ ;
$\gamma \in [0, 1]$ 是折扣因子;
为了缓解过拟合,引入 double-DQN 的结构,所以公式 7 被重写为:
$$ y_t = r(s_t, a_t) + \gamma Q(s_{t+1}, {\pi}(s_{t+1}; \theta); {\theta}’) $$
利用公式 6 和公式 8 可以得出 $i^{th}$ 维的暂时损失函数:
$$ l^i_t = Q_{target} - Q(u^i_{s_t}, a^i_t; \theta), \forall i \in [0, …N-1] $$
其中 $Q_{target}$ 满足:
$$ Q_{target} = r_t + {\gamma}_u \cdot Q(u^0_{s_{t+1}}, \pi(u^0_{s_{t+1}}; 0); {\theta}’) $$
${\gamma}_u$ 和 ${\gamma}_b$ 分别代表”Top MDP“和”Bottom MDP“的折扣因子,训练中设定 ${\gamma}_b = 1$ 。
观察公式 9 和公式 10 可以看出每维都有相同的目标函数,意味着无法区别每个独立维度的动作 $a^i_t$ 对 $r_t$ 的贡献。
为了克服限制,根据某个分块的动作 $a^i_t$ 与其观看概率成正比的先验知识,向 $l^i_t$ 添加一个额外的 $r^i_{extra}$ :
$$ l^i_t = r^i_{extra} + Q_{target} - Q(u^i_{s_t}, a^i_t; \theta), \forall i \in [0, …N-1] $$
$$ r^i_{extra} = \begin{cases} 0, p_i > P ; \ -a^i_t, p_i \le P \end{cases} $$
通过设定一个观看概率的阈值 $P$ ,对观看概率低于 $P$ 但选择了高码率的分块施加 $-a^i_t$ 的奖励。
因此最终的平均损失可以形式化为:
$$ l^{avg}_t = \frac{1}{N} \sum^{N-1}_{i=0} l^i_t $$
接着使用梯度下降法来更新模型,学习率设定为 $\alpha$:
$$ \theta \larr \theta + \alpha \triangledown l^{avg}_t $$
同时,在训练阶段利用经验回放法来提高360SRL的泛化性。


实现细节
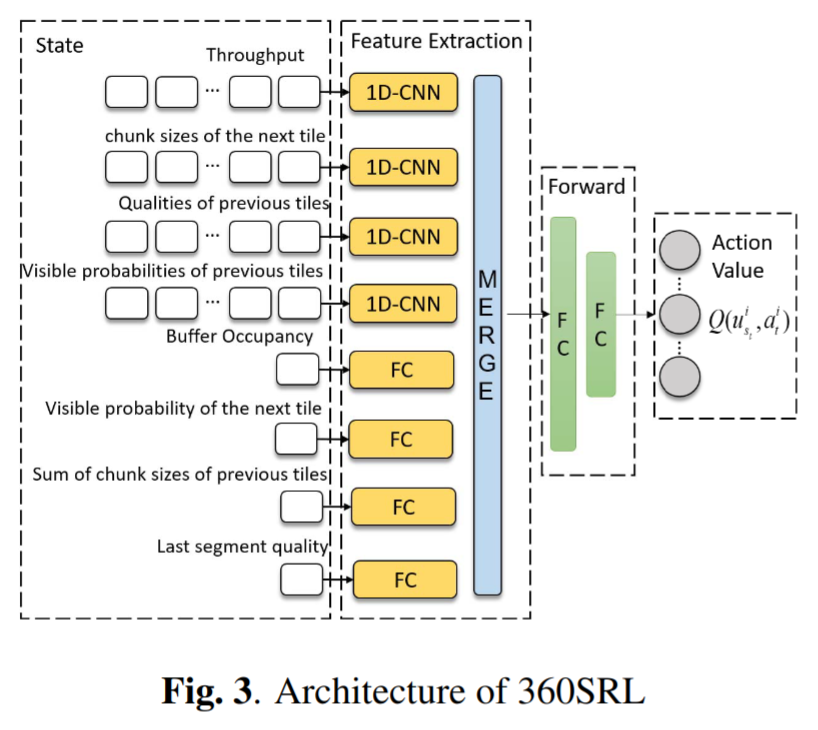
特征从输入状态中通过特征提取网络提取出来。
初始的 4 个输入通过带有 128 个过滤器的 1 维卷积层被传递,4 个输入核心大小分别为 $1 \times m$ 、 $1 \times M$ 、 $1 \times N$ 、 $1 \times M$ ,后续这 4 个输入被喂给有 128 个神经元的全连接层;
随后特征映射被连接成一个张量,接着是具有 1024 个神经元和 256 个神经元的前向网络;
整个动作-价值网络的输出是 M 维的向量。
特征提取层和前向网络层都使用 Leaky-ReLU作为激活函数,最后是层归一化层。