论文概况
Link: https://dl.acm.org/doi/10.1145/3232565.3234686
Level: SIGCOMM 18
Keyword: UDP+FOV-aware+FEC
工作范围
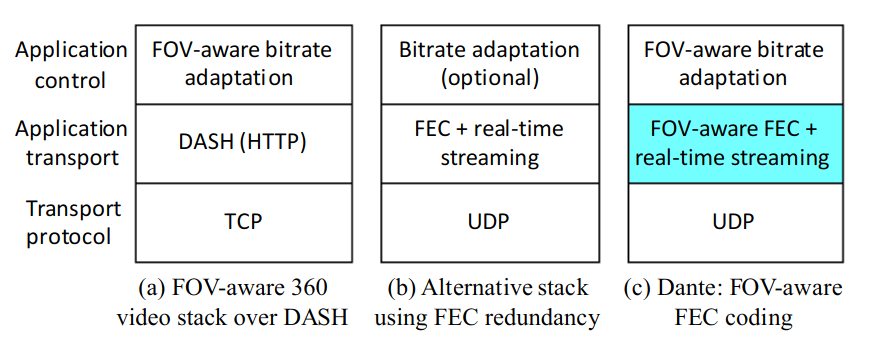
目标
在给定序列的帧中,为每个 tile设定 FEC 冗余,根据其被看到的可能性的加权最小化平均质量降低。
问题建模
输入 估计的丢包率$p$、发送速率$f$、有$n$个 tile 的$m$个帧($<i, j>$来表示第$i$个帧的第$j$个 tile
第$<i, j>$个 tile 的大小$v_{i, j}$、第$<i, j>$个 tile 被看到的可能性$\gamma_{i, j}$、
如果第$<i, j>$ 个 tile 没有被恢复的质量降低率、最大延迟$T$
输出
第$<i, j>$个 tile 的 FEC 冗余率$r_{i, j} = \frac{冗余包数量}{原始包数量}$
最优化问题的形式化
$$ minimize\ \sum_{0<i\le m}\sum_{0<j\le n} \gamma_{i, j}d_{i, j}(p, r_{i, j}) $$
$$ subject\ \ to\ \ \frac{1}{f}\sum_{0<i\le m}\sum_{0<j\le n}v_{i, j}(1+r_{i, j}) \le T $$
$$ r_{i, j} \le 0 $$
(1):最小化最终被看到的 tile 的质量衰减的加权和,权重按照被看到的可能性分配。
(2):经过重新编码的包和原始的包需要在 T 时刻之前发出。
Dante 将 1 个 GOP(Group of Pictures)中的所有帧当作一批处理,$T$作为 GOP 的持续时间
$f$:使用 TCP Friendly Rate Control algorithm,基于估计的丢包率和网络延迟来计算得出
(3):确保冗余率总是非负的。
关键变量是$d_{i, j}(p, r)$:丢包率是 p 情况下,采用 r 作为冗余率的第$<i, j>$个 tile 的质量衰减
$$ d_{i, j}(p, r) = \delta_{i, j},\ if\ r < \frac{1}{1-p}; 0, otherwise. $$
假设帧中有 k 个原始包,质量衰减发生在丢失的包不能被恢复的情况下。
FEC 可以容忍 $r \cdot k$ 个丢包=>即当 $p(rk+k)$ 大于 $rk$ 时会发生质量衰减。
过多的丢包会导致依赖链上所有帧的质量衰减,因此考虑帧之间的依赖关系之后,可以重新计算质量衰减:
$$ d^{*}{i, j}(p, r) = \sum{0<c\le i}w_{c, i}d_{c, j}(p, r) $$
$w_{c, i}$ 编码帧 i 对帧 c 的依赖作为单独的第 c 个帧的质量衰减的权重;
最终第 i 个帧的第 j 个 tile 的最终质量衰减就是所有依赖的质量衰减的和。
FEC 冗余的自适应逻辑
关于$d_{i, j}(p, r)$ :因为是分段函数,所以其值会因为 r 和 p 的大小关系而急剧改变。
利用背包问题的思想可以将其规约成 NP 完全问题:
将每个 tile 看作是一个物品,共有 m*n 个。
如果$r_{i, j} < \frac{1}{1-p}$ ,则表示不把第<i,j>和物品放入背包;否则就是将其放入背包。
公式 1 可以转化为:最大化所有物品二元变量的线性组合;
公式 2 可以转化为:二元变量的另一个线性组合必须低于阈值约束。
因此整个问题就能被完全转化为0-1 背包问题
算法

整体上是背包问题的标准解法,能以线性复杂度(因为变量只是 B)解决问题。
原型设计
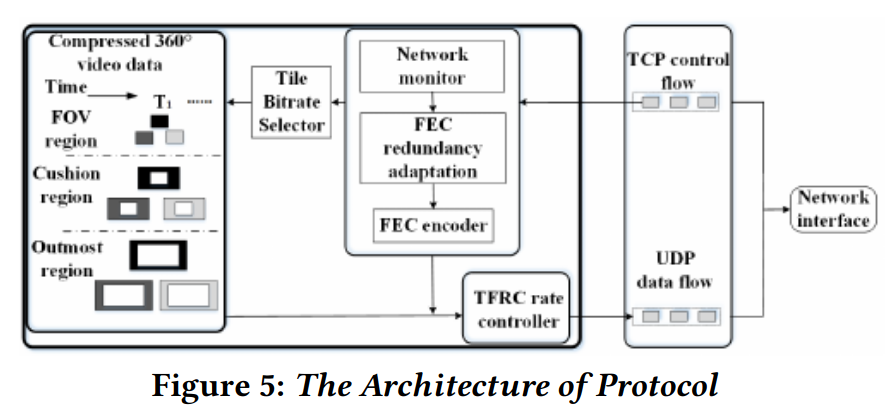
- 使用基于 TCP 和 UDP 的两条连接来分别传输控制信息(双向:到客户端的播放会话的起至点和到服务端的网络信息反馈)和视频数据包
- 服务端根据反馈的网络信息,在每个 GOP 的边界时刻运行算法 1 来确定下一个 GOP 的帧和 tile 的 FEC 冗余。 确定之后服务端使用 RS 码来插入冗余包,和原始视频数据包一起重新编码,并使用基于 TFRC 的发送率发送数据。
- Dante 的实现是对应用程序级比特率适配策略的补充,并且可以通过对视频播放器进行最小更改来替换现有的底层传输协议来部署。
实验评估
环境:使用 Gilbert 模型来模拟实现丢包事件(而非使用统一随机丢包)
创造了两种网络条件 good(丢包率 0.5%)和 bad(丢包率 2%)
局限性
- 效果主要依赖于 Viewport 预测的结果是否准确