论文概况
Link:A Control-Theoretic Approach for Dynamic Adaptive Video Streaming over HTTP
Level:ACM SIGCOMM 15
Keywords:Model Predictive Control,ABR,DASH
Motivation
关于码率自适应的逻辑,现有的解决方案还没有形成清晰的、一致的意见。不同类型的方案之间优化的出发点并不相同,比如基于速率和基于缓冲区,而且没有广泛考虑各方面的因素并形成折中。
文章引入了控制论中的方法,将各方面的影响因素形式化为随机优化控制问题,利用模型预测控制 MPC将两种不同出发点的解决方案结合到一起,进而解决其最优化的问题。而仿真结果也证明,如果能运行一个最优化的 MPC 算法,并且预测误差很低,那么 MPC 方案可以优于传统的基于速率和基于缓冲区的策略。
背景
- 播放器端为 QoE 需要考虑的问题:
- 最小化冲缓冲事件发生的次数;
- 在吞吐量限制下尽可能传输码率较高的视频;
- 最小化播放器开始播放花费的时间(启动时间);
- 保持播放过程平滑,尽可能避免大幅度的码率变化;
- 这些目标相互冲突的原因:
- 最小化重缓冲次数和启动时间会导致只选择最低码率的视频;
- 尽可能选择高码率的视频会导致很多的重缓冲事件;
- 保持播放过程平滑可能会与最小的重缓冲次数与最大化的平均码率相冲突;
控制论模型
视频推流模型
参数形式化
将视频建模成连续片段的集合,即:$V = \lbrace 1, 2, …, K \rbrace$,每个片段长为$L$秒;
每个片段以不同码率编码,$R$ 作为所有可用码率的集合;
播放器可以选择以码率$R_k \in R$ 下载第$k$块片段,$d_k(R_k)$ 表示以码率$R_k$编码的视频大小;
- 对于恒定码率 CBR 的情况,$d_k(R_k) = L \times R_k$;
- 对于变化码率 VBR 的情况,$d_k \sim R_k$;
选择的码率越高,用户感知到的质量越高:
$q(\cdot):R \rightarrow \R_+$ 是一个不减函数,是选择的码率 $R_k$ 到用户感知到的视频质量 $q(R_k)$ 的映射;
片段被下载到回访缓冲中,其中包含下载了的但还没看过的片段。
$B(t) \in [0, B_{max}]$ 表示 $t$ 时刻缓冲区的占用, $B_{max}$ 表示内容提供商的策略和播放器的存储限制;
播放过程形式化
在 $t_k$ 时刻,视频播放器开始下载第 $k$ 个块,这个块的下载时间可以计算为: $d_k(R_k) / C_k$; $C_k$ 表示下载过程中经历的平均下载速度;
一旦第 $k$ 个块下载完毕,播放器等待 $\Delta t_k$ 时间并在 $t_{k+1}$ 时刻下载下一个块 $k+1$ ;
假设等待时间 $\Delta t_k$ 很短并且不会导致重缓冲事件,用 $C_t$ 表示 $t$ 时刻的网络吞吐量:
$$ t_{k+1} = t_k + \frac{d_k(R_k)}{C_k} + \Delta t_k $$
$$ C_k = \frac{1}{t_{k+1} - t_k - \Delta t_k} \int_{t_k}^{t_{k+1} - \Delta t_k} C_t dt $$
$B(t)$ 的变化取决于下载的块和播放的块的数量:
在第 $k$ 个块下载完毕之后缓冲区占用增长 $L$ 秒;用户观看一个块之后缓冲区占用减少 $L$ 秒;
$B_k = B(t_k)$ 表示播放器开始下载第 $k$ 个块时的缓冲区占用;
缓冲区占用的动态变化可以表示为:
$$ B_{k+1} = \big( (B_k - \frac{d_k(R_k)}{C_k})_+ + L - \Delta t_k \big)_+ $$
其中 $(x)_+ = max\lbrace x, 0 \rbrace $ 确保其非负;
如果 $B_k < d_k(R_k) / C_k$ ,表示缓冲区在播放器还在下载第 $k$ 个块时变空,而这会导致重缓冲事件;
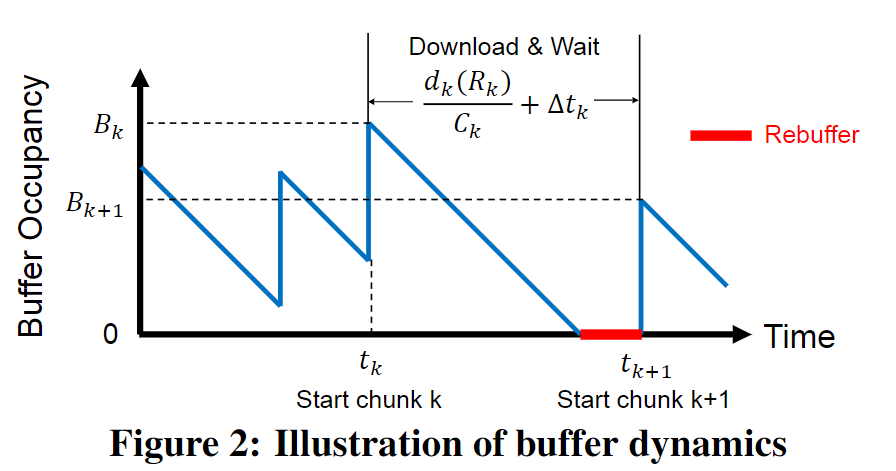
等待时间 $\Delta t_k$ 的确定也称为块调度问题,本文中假设播放器在第 $k$ 个块下载完毕之后尽可能快地去下载第 $k+1$ 个块(除了缓冲区满了的情况,播放器等待缓冲区中的块被消耗之后再下载新的块):
$$ \Delta t_k = \Big( \big( B_k - \frac{d_k(R_k)}{C_k} \big)_+ + L - B_max \Big)_+ $$
QoE 最大化问题
QoE 的组成部分:
平均视频质量:在所有块中每个块平均的质量,计算为:
$$ \frac{1}{K} \sum^K_{k=1} q(B_k) $$
平均质量变化:相邻块之间质量变化的平均值,计算为:
$$ \frac{1}{K-1} \sum^{K-1}_{k=1} | q(R_{k+1}) - q(R_k) | $$
重缓冲总计时间:对每个块而言,当轮到其被消耗时但下载块的过程还没完成即出现了重缓冲,总时间计算为:
$$ \sum^K_{k=1} (\frac{d_k(R_k)}{C_k} - B_k)_+ $$
启动延迟 $T_s$ ,假设 $T_s \ll B_{max}$ 。
对不同用户而言,上述 4 种因素的重要程度不同。使用上述分量的加权,定义视频块 $1$ 到 $K$ 的 QoE:
$$ QoE^K_1 = \sum^K_{k=1} q(R_k) - \lambda \sum^K_{k=1} | q(R_{k+1}) - q(R_k) | - \mu \sum^K_{k=1} (\frac{d_k(R_k)}{C_k} - B_k)_+ - \mu_s T_s,\ \lambda, \mu, \mu_s \nless 0 $$
相对较小的 $\lambda$ 表示用户不太关心视频质量变化; $\lambda$ 越大表明越需要使视频质量变得光滑。
相对较大的 $\mu$ 表示用户很在意重缓冲;
在这里文章倾向于启动延迟很低,所以采用大 $\mu_s$ ;
QoE 的最大化:
输入:吞吐量迹 ${C_t, t \in [t_1, t_{K+1}]}$
输出:码率选择 $R_1, …, R_K$;启动时间 $T_s$ ;
需要注意:当最大化的决策发生在播放过程中时,启动时间便不再存在;

算法
上图中的 QoE 最大化问题是一种随机优化控制问题,随机性源自可获得的吞吐量 $C_t$ 。
$t_k$ 时刻播放器选择码率 $R_k$ ,只有过去的吞吐量 $\lbrace C_t, t \le t_k \rbrace$ 可知,未来的值 ${C_t, t > t_k}$ 未知。
但是,吞吐量预测器可以用于获取对吞吐量的预测,定义其为 $\lbrace \hat{C_t}, t > t_k \rbrace$ 。
基于这样的预测和缓冲区的信息(精确可知),码率选择器对下个块 $k$ 的码率选择可以表示为:
$$ R_k = f \big( B_k, \lbrace \hat{C_t}, t > t_k \rbrace, \lbrace R_i, i < k \rbrace \big) $$
文章只关注码率自适应算法,假设已经得到了预测值,并根据预期预测误差对其进行了表征,即:
我们着重于 $f(\cdot)$ 的设计以及预测误差对比较控制算法性能的影响。
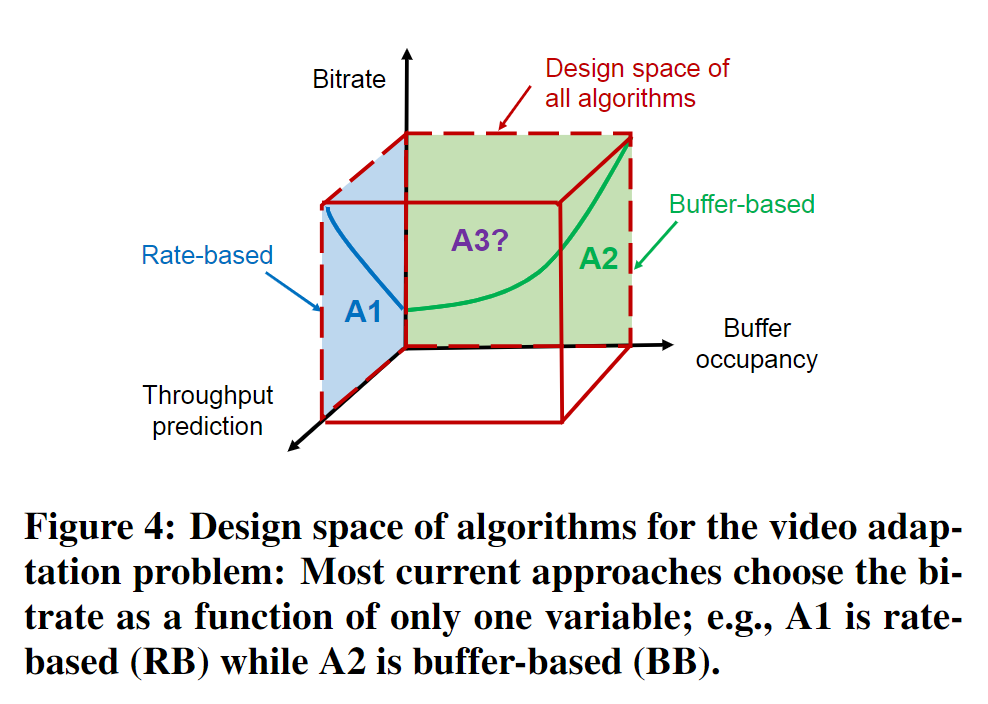
现有的两类自适应算法:基于速率和基于缓冲区,分别可以表示为:
$$ R_k = f \big( \lbrace \hat{C_t}, t > t_k \rbrace, \lbrace R_i, i < k \rbrace \big) $$
$$ R_k = f(B_k, \lbrace R_i, i < k \rbrace) $$
前者只基于吞吐量的预测结果而不管缓冲区状况;后者只基于缓冲区而不管未来的吞吐量可能状况;
这两种方法在原则上都只是次优的,理想情况下我们想要同时考虑缓冲区占用和吞吐量预测结果。
MPC for Optimal Bitrate Adaptation
Why MPC
MPC 天然适合码率自适应问题。
Strawman solutions
码率自适应问题本质是随机控制优化问题,就这一点而言,有两个知名控制算法:
- Proportional-integral-derivation(PID) control.
- Markov Decision Process(MDP) based control.
PID 相较 MDP 而言计算起来更加简单,只能用于使系统稳定,不能显式地优化 QoE 目标;此外 PID 被设计用于有连续的时间和连续的状态空间的问题中,用于当前这种高度离散化的问题中会导致性能亏损和不稳定。
应用 MDP 的话可以将吞吐量和缓冲区状态形式化为马氏过程,然后使用诸如值迭代和策略迭代等标准算法求出最优解。
(然而,这有一个很强的假设,即吞吐量动态遵循马尔可夫过程,不清楚这在实践中是否成立。我们将 MDP 的潜在用途和吞吐量动态分析作为未来的工作。)
Case for MPC
理想情况下,如果给出未来吞吐量的完美数据,那么启动时间 $T_s$ 和最优码率选择 $R_1, … R_K$ 可以一下子就计算出来;
实际情况中,虽然不能得到未来吞吐量的完美预测,但是我们可以假设吞吐量在较短的时间段 $[t_k, t_{k+N}]$ 内不会剧烈变化。
基于此,可以使用当前视界中的预测来应用第 1 个码率 $R_k$ ,之后将视界向前移动到 $[t_{k+1}, t_{k+N+1}]$ 。
而这种方案就称为 MPC。MPC 的一般好处在于,MPC 可以利用预测在约束条件下在线优化动态系统中的复杂控制目标。