论文概况
Link:OpTile: Toward Optimal Tiling in 360-degree Video Streaming
Level:ACM MM 17
Keyword:Dynamic tile division, Optimize encoding efficiency, Optimize tile size
背景知识
编码过程概述
对一帧图像中的每一个 block,编码算法在当前帧的已解码部分或由解码器缓冲的临近的帧中搜索类似的 block。
当编码器在邻近的帧中找到一个 block 与当前 block 紧密匹配时,它会将这个类似的 block 编码进一个动作向量中。
编码器计算当前 block 和引用 block 之间像素点的差异,通过应用变换(如离散余弦变换),量化变换系数以及对剩余稀疏矩阵系数集应用无损熵编码(如 Huffman 编码)对计算出的差异进行编码。
对编码过程的影响
- 基于 tile 的方式会减少可用于拷贝的 block 数量,增大了可供匹配的 tile 之间的距离。
- 不同的投影方式会影响编码变换输出的系数稀疏性,而这会降低视频编码效率。
投影过程
因为直接对 360 度图像和视频的编码技术还没有成熟,所以 360 度推流系统目前还需要先将 3D 球面投影到 2D 平面上。
目前应用最广的投影技术主要是 ERP 和 CMP,分别被 YouTube 和 Meta 采用。
ERP 投影
基于球面上点的左右偏航角$\theta$与上下俯仰角$\phi$将其映射到宽高分别为$W$和$H$的矩形上。
对于平面坐标为$(x, y)$的点,其球面坐标分别为:
$$ \theta = (\frac{x}{W} - 0.5) * 360 $$
$$ \phi = (0.5 - \frac{y}{H}) * 180 $$
CMP 投影
将球面置于一个立方体中,光线从球心向外发射,并分别与球面和立方体相交于两点,这两点之间便建立了映射关系。
之后将立方体 6 个平面拼接成矩形,就可以使用标准的视频编码方式进行压缩。
关于投影方式还可以参考这里的讲解:谈谈全景视频投影方式
tile 方式的缺点
降低编码效率
tile 划分越细,编码越低效
增加更大的整体存储需求
可能要求更多的带宽
OpTile 的设计
直觉上需要增大一些 tile 的大小来使与这些 tile 相关联的片段能捕获高效编码所需的类似块。
同时也需要 tile 来分割视频帧来减少传输过程中造成的带宽浪费。
为了明白哪些片段的空间部分可以被高效独立编码,需要关于 tile 的存储大小的不同维度的信息。
为了找到切分视频的最好位置,需要在片段播放过程中用户 viewport 运动轨迹的偏好。
将编码效率和浪费数据的竞争考虑到同一个问题之中,这个问题关注的是一个片段中所有可能的视图的分布。
片段的每个可能的视图可以被 tile 的不同组合所覆盖。
目标是为一个片段选择一个 tile 覆盖层,以最小化固定时间段内视图分布的总传输带宽。
- 目标分离的部分考虑整个固定时间段的表示(representation)的存储开销。
- 目标的存储部分与下载的带宽部分相竞争。例如,如果一个不受欢迎的视频一年只观看一次,那么我们更喜欢一个紧凑的表示,我们可以期望向用户发送更多未观看的像素。
问题形式化
| segment/片段 | 推流过程中可以被下载的连续播放的视频单元 |
|---|---|
| basic sub-rectangle/基本子矩形 | 推流过程中可以被下载的片段中最小的空间划分块 |
| solution sub-rectangle/解子矩形 | 片段中由若干基本子矩形组成的任何矩形部分 |
| $x$ | 用于表示子矩形在解中的存在的二元向量 |
|---|---|
| $c^{(stor)}$ | 每个子矩形存储开销相关的向量 |
| $c^{(view)}$ | 给定一个 segment 中用户 viewport 的分布,$c^{(view)}$指相关子矩形的预期下载字节 |
| $\alpha$ | 分配到$c^{(view)}$的权重,以此来控制相对于传输一个片段的存储开销 |
考虑将 1 个矩形片段划分成 4 个基本子矩形,其对应的坐标如下:
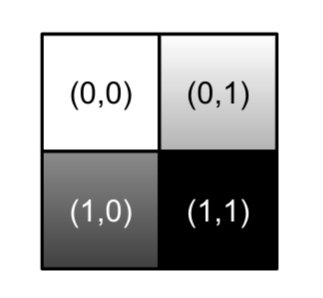
4 个基本子矩形可以有 9 种分配方式,成为解子矩形,如下(因为需要保持对应的空间关系,所以只有 9 种):
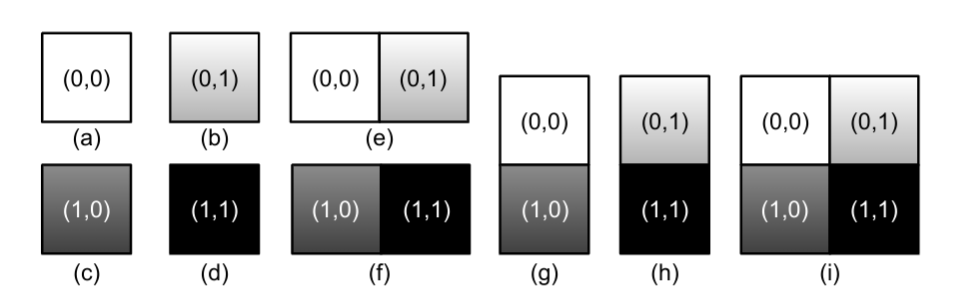
$x$的形式化
可以用向量$x$来分别表示上图中子矩形在解中的存在:
$$ [1 \times 1\ at\ (0, 0),\ 1 \times 1\ at\ (0, 1),\ 1 \times 1\ at\ (1, 0), \ 1 \times 1\ at\ (1, 1),\ 1 \times 2\ at\ (0, 0),\ 1 \times 2\ at\ (1, 0), \ 2 \times 1\ at\ (0, 0),\ 2 \times 1\ at\ (0,1),\ 2 \times 2\ at\ (0,0).] $$
($x$中每个二元变量的的组成:$1 \times 1$表示子矩形的形状,$(0,0)$表示所处的位置)
要使$x$有效,每个基本子矩形必须被$x$中编码的子矩形精确覆盖一次。例如:
$[0, 0, 0, 0, 1, 1, 0, 0, 0]$=>有效(第 5 和第 6 次序的位置分别对应$e$和$f$子矩形,恰好覆盖了所有基本子矩形 1 次)
$[0,0,0,1,1,0,0,0,0]$=>无效(第 4 和第 5 次序的位置分别对应$d$和$e$子矩形,没有覆盖到$(1,0)$基本子矩形)
$[0,0,0,1,1,1,0,0,0]$=>无效(第 4、第 5 和第 6 次序的位置分别对应$d$、$e$和$f$子矩形,$(1,1)$基本子矩形被覆盖了两次)
$c^{(stor)}$的形式化
与每个$x$相对应的向量$c^{(stor)}$长度与$x$相等,其中每个元素是$x$中对应位置的子矩形的存储开销的估计值。
$c^{(view)}$的形式化
考虑分发子矩形的网络带宽开销时,需要考虑所有可能被分发的 360 度表面的视图。
为了简化问题,将片段所有可能的视图离散化到一个大小为$V$的集合中。
集合中每个元素表示一个事件,即向观看 360 度视频片段的用户显示基本子矩形的唯一子集。
注意到片段中被看到的视频区域可以包含来自多个视角的区域。
将之前离散化好的大小为$V$的集合中每个元素与可能性相关联:$[p_1, p_2, …, p_V]$。
考虑为给定的解下载视图$V$的开销,作为需要为该视图下载的数据量:
$$ quantity = x^{\top}diag(d_v)c^{(stor)} $$
$d_v$是一个二元向量,其内容是按照$x$所描述的表示方案,对所有覆盖视图的子矩形的选择。
例如对于 ERP 投影中位置坐标为$yaw = 0, pitch = 90$即处于等矩形顶部的图像,对应的$d_{view-(0, 90)} = [1, 1, 0, 0, 1, 0, 1, 1, 1]$
(即上面图中$a, b, e, g, h, i$位置的子矩形包含此视图所需的基本子矩形)。
给出一个片段中的用户 viewport 分布,$c^{(view)}$的元素是相关联的子矩形预期的下载字节。
$$ c^{(view)} = \sum_v p_v diag(d_v) c^{(stor)} $$
最后,将优化问题的基本子矩形覆盖约束编码为矩阵$A$。
$A$是一个列中包含给定子矩形解所覆盖的基本子矩形信息的二元矩阵。
对于$2 \times 2$的矩形片段,其$A$有 4 行 9 列,例子如下:

因此最终的问题可以形式化为一个整数线性程序:
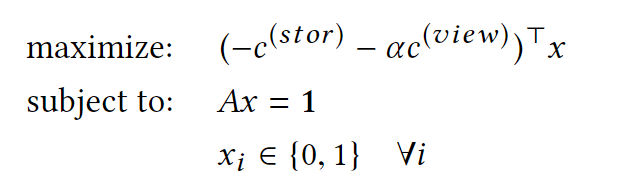
$c^{(stor)}$
可以理解为存储一段$\Delta t$时间长的片段的子矩形的存储开销;
$c^{(view)}$
可以理解为传输一个视图所需要的所有的子矩形的传输开销。
$\alpha$
控制相比于传输一个片段的相对存储开销,同时应该考虑片段的流行度。
即$\alpha$应该与所期望的片段在$\Delta t$的时间间隔内的下载次数成比例,$\alpha$应该可以通过经验测量以合理的精度进行估计。
可以通过将$x$的二元离散限制放松到$0 \le x_i \le 1\ \forall i$构成一个线性程序,其解为整数。
(对于有 33516 个变量的$x$,其解可以在单核 CPU 上用 7~10 秒求出)
开销向量建构
首先需要建构出存储开销向量$c^{(stor)}$,但是对于有$n$个基本子矩形的子矩形,其建构复杂度为$O(n^2)$。
因此对每个子矩形进行编码来获得存储开销并不可行,所以利用视频压缩与运动估计之间的强相关性来预测$c^{(stor)}$的值。
给定一个视频,首先暂时将其分成长度为 1 秒的片段,每个片段被限定为只拥有 1 个 GOP,片段的大小表示为$S_{orig}$。
接着抽取出每个片段中的动作序列用于之后的分析。
将片段从空间上划分成基本子矩形,每个基本子矩形包含$4 \times 4 = 16$个宏块(例如:$64 \times 64$个像素点)。
独立编码每个基本子矩形,其大小表示为$S_i$。
通过分析动作向量信息,可以推断出如果对基本子矩形$i$进行独立编码,指向基本子矩形$i$的原始运动向量应该重新定位多少。
将其表示为$r_i$。
每个运动向量的存储开销可以计算为:
$$ o = \frac{\sum_i S_i - S_{orig}}{\sum_i r_i} $$
即:存储开销的整体增长除以被基本子矩形边界所分割的运动向量数。
如果基本子矩形被融合进更大的子矩形$t$,使用$m_t$来表示由于融合操作而无须再进行重定位的运动向量的数量:
$$ m_t = \sum_{i \in t} r_i - r_t $$
$i \in t$表示基本子矩形位于子矩形$t$中。
为了估计任意子矩形$t$的大小,使用下面 5 个参数: $$ \sum_{i \in t} S_i,\ \sum_{i \in t} r_i,\ m_t,\ o,\ n $$ $n$表示$t$中基本子矩形的数量。
实际操作:
创建了来自 4 个单视角 360 度视频的 6082 个 tile 数据集。4 个视频都以两种分辨率进行编码:$1920 \times 960$和$3980 \times 1920$。
为了产生 tile,从视频中随机选取片段,随机选取 tile 的位置,宽度和高度。
设置 tile 的 size 最大为$12 \times 12$个基本子矩形。
对于每个选择的 tile,为其建构一个数据集元素:
- 计算上面提到的 5 参数的特性向量。
- 使用 FFmpeg 编码 tile 的视频段来得到存储该段需要的空间。
使用多层感知机 MLP 来估计 tile 的大小。
MLP 中包含 50 个节点的单隐层,激活函数为 ReLU 函数,300 次迭代的训练过程使用L-BFGS 算法。
为了评估 MLP 的预测效果,使用 4 折的交叉验证法。
每次折叠时先从 3 个视频训练 MLP,接着使用训练好的模型去预测第 4 个视频的 tile 大小。
实现
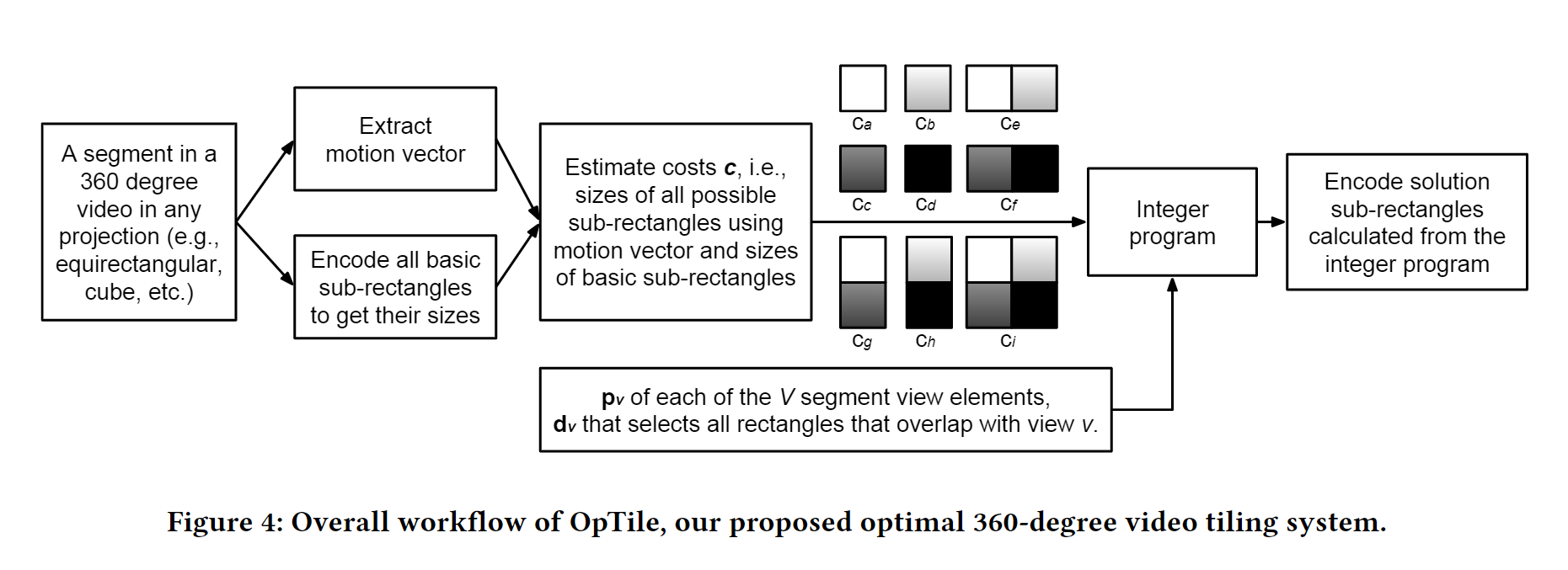
将视频划分成 1 秒长的片段,之后为每个片段解决整数线性问题来确定最优的 tile 划分策略。
- 使用 MLP 模型估计每个 tile 的存储开销。
- 根据视图的集合$d$及其对应的可能性分布$p$,来估计视图的下载开销$c^{(view)}$。
- 构造矩阵$A$时,限制最大的 tile 大小为$12 \times 12$的基本子矩形(如果设置每个基本子矩形包含$64 \times 64$的像素,tile 的最大尺寸即为$768 \times 768$的像素)。
- 使用GNU Linear Programming Kit来解决问题。
- 将所有可能的解子矩形编码进一个二元向量$x$中来表示解。
- GLPK 的解表明一个可能的解子矩形是否应该被放入解中。
- 基于最终得到的解,划分片段并使用 ffmepg 以同样参数的 x264 格式进行编码。
评估
度量指标
- 服务端存储需求。
- 客户端需要下载的字节数。
数据来源
评估准备
下载 5 个使用 ERP 投影的视频,抽取出测试中用户看到的对应部分。
每个视频都有$1920 \times 960$和$3840 \times 1920$的两种分辨率的版本。
$1920 \times 960$视频的基本子矩形尺寸为$64 \times 64$的像素。
$3840 \times 1920$视频的基本子矩形尺寸为$128 \times 128$的像素。
将视频划分成 1 秒长的片段,对每个片段都产生出 MLP 所需的 5 元组特性。
之后使用训练好的 MLP 模型来预测所有可能的 tile 的大小。
数据选择
从数据集中随机选择出 40 个用户的集合。
假设 100°的水平和垂直 FOV,并使用 40 个用户的头部方向来为每个片段产生$p_v$和$d_v$。
即:分块的决策基于每个片段的内容特征信息与用户的经验视图模式。
参数设定:$\alpha = 0,1,1000$.
对比实验:
一组使用由 ILP 得出的结构进行分块;
另外一组:
$1920 \times 960$的视频片段分别使用$64 \times 64$,$128 \times 128$,$256 \times 256$,$512 \times 512$的方案固定大小分块。
$3840 \times 1920$的视频片段分别使用$128 \times 128$,$256 \times 256$,$512 \times 512$,$1024 \times 1024$的方案固定大小分块。
划分结果对比
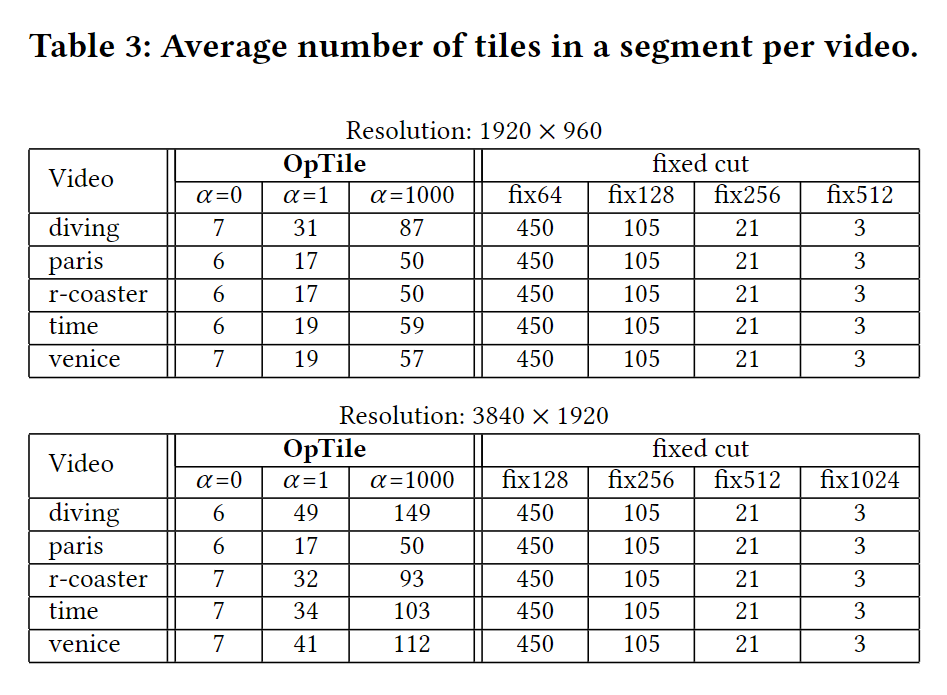
服务端的存储大小
按照$\alpha = 0$方案分块之后的视频大小几乎与未分块之前的视频大小持平,有时甚至略微小于未分块前的视频大小。
因为所有分块方案都使用相同的编码参数,所以重新编码带来的有损压缩并不会影响竞争的公平性。
如果将$\alpha$的值调大,存储的大小会略微增大;固定分块大小的方案所得到的存储大小也会随 tile 变小而变大。
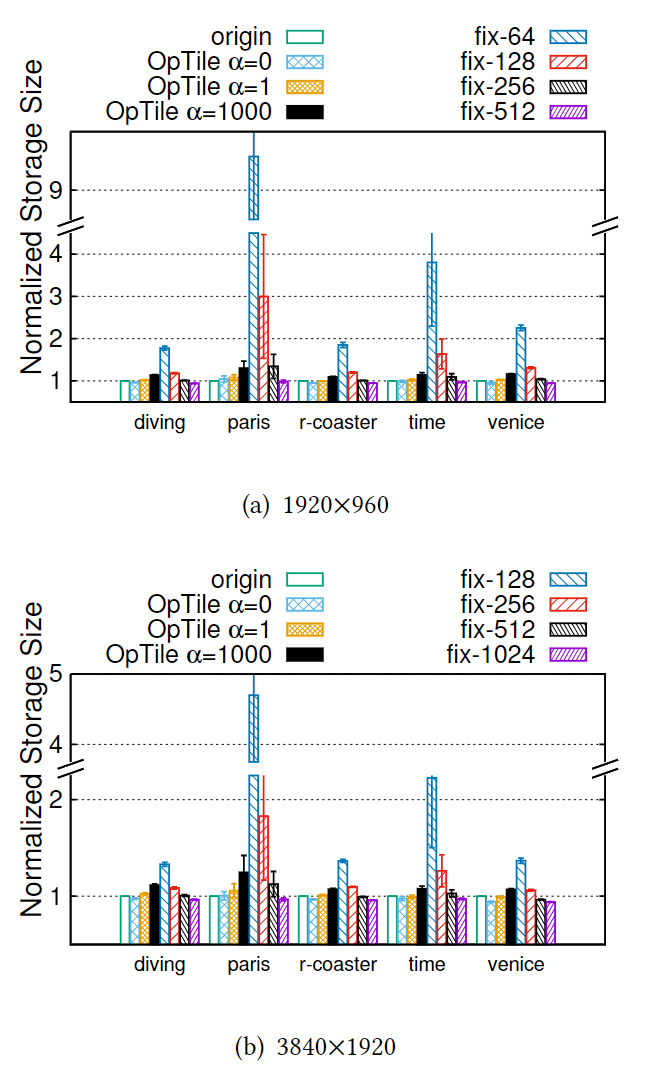
客户端的下载大小
预测完美的情况——下载的 tile 没有任何浪费
$\alpha= 1000$的情况下,OpTile 的表现总是最好的。
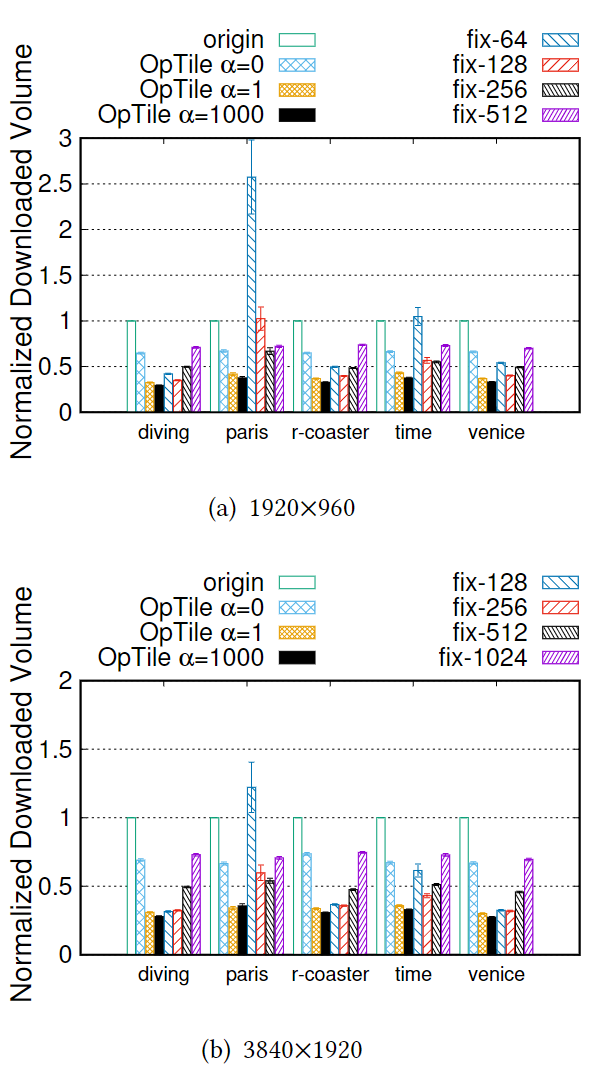
正常预测的情况
预测的方法:假设用户的头部方向不会改变,预测的位置即为按照当前方向几秒之后的位置。
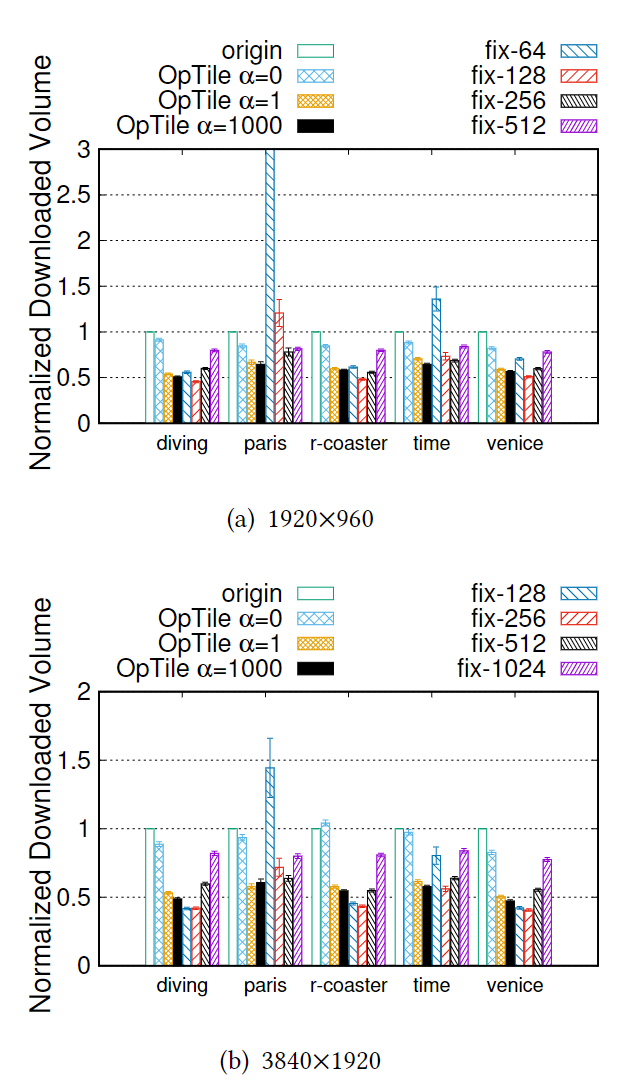
相比于完美假设的预测,所有分块方案的下载大小都增大了。
$\alpha = 1000$的方案在两个视频的情况下都取得了最小的下载大小。在剩下的 3 个视频中,OpTile 方案的下载大小比起最优的固定分块大小方案不超过 25%。
尽管固定分块大小的方案可能表现更好,但是这种表现随视频的改变而变化显著。
因为固定分块的方案没有考虑视频内容的特性与用户的观看行为。