论文概况
Link:Popularity-Aware 360-Degree Video Streaming
Level:IEEE INFOCOM 2021
Keywords:Dynamic tiling, Cross-user division, Heuristic QoE optimization
Motivation
将视频划分成分块进行编码之后,会降低编码效率,并增大服务端的存储压力。(细节可以参见Optile)
而分块时根据用户的 ROI 来确定不同的大小,并在客户端预取,这可以节省带宽。
用户的 ROI 推断利用跨用户的偏好来确定,即所谓的Popularity-Aware。
Model and Formulation
Video Model
视频从时间上被分成固定长度的片段,接着每个片段被从空间上划分成 $C$ 个分块。
除了常规的分块之外, $M$ 个宏块也被建构出来。
每个常规分块和宏块都被编码成 $V$ 个不同的码率质量等级并存储在服务端。
整个推流过程可以看作是一系列连续的下载任务。
客户端在每次下载任务中的目标是:选择恰当分块(宏块或者常规分块的集合)的恰当质量。
用 $L$ 表示客户端请求分块时,缓冲区中已经下载但还没有查看的视频的视频长度,为了避免缓冲事件,分块需要在缓冲区被清空即 $L = 0$ 之前被下载完毕。
QoE Model
$$ Q(V_k) = Q_{0}(V_k) - {\omega}_v I_v (V_k) - {\omega}_r I_r (V_k) $$
$V_k$ 表示下载的第 $k$ 段视频质量; $Q_0$ 表示平均质量; $I_v$ 表示由质量变化导致的质量损害; $I_r$ 表示由缓冲事件导致的质量损害; ${\omega}_v$ 和 ${\omega}_r$ 分别表示质量变化和缓冲的加权因子;
平均质量:
$$ Q_0(V_k) = q(\overline{V_k}) $$
$\overline{V_k}$ 表示
FoV内的平均视频质量; $q(\cdot)$ 表示视频质量和用户实际感知质量之间的映射函数;质量变化:两个连续段之间的质量差异和
FoV内不同空间位置 tile 的质量差异会导致用户不适。$$ I_v(V_k) = |Q_0(V_k) - Q_0(V_{k-1})| + \widehat{V_k} $$
$|Q_0(V_k) - Q_0(V_{k-1})|$ 表示连续段间的
FoV内时间质量差异; $\widehat{V_k}$ 表示一个视频段的FoV内空间质量差异;缓冲: $$ L_r(V_k) = {(\frac{S(V_k)}{R} - L, 0)}_+ $$ $S(V_k)$ 表示段数据量大小; $R$ 表示下载吞吐量; ${(x)}_+ = max \lbrace x, 0 \rbrace$ ;
Formulation
用 ${\beta}^v_m ({\beta}^v_c)$ 表示对应的宏块或常规块是否被下载:
${\beta}^v_m = 1$ 表示下载编码的质量等级为 $v$ 的宏块,消耗的带宽为 $B^v_m$ ,反之 $ {\beta}^v_m = 0$ 表示不下载;
${\beta}^v_c = 1$ 表示下载编码的质量等级为 $v$ 的常规块,消耗的带宽为 $B^v_c$,反之 ${\beta}^v_m = 0$ 表示不下载;
客户端应该优先下载覆盖用户FoV 的宏块,如果没有这样的宏块则去下载对应的常规块的集合。
优化目标:
$$ max\ Q(\lbrace v | {\forall}_{m, v} {\beta}^v_m = 1 \rbrace) + Q(\lbrace v | {\forall}_{c, v} {\beta}^v_c = 1 \rbrace) $$
同时需要满足以下 3 个约束:
$$ \sum^{M}_{m=1} \sum^{V}_{v=1} {\beta}^v_m + 1(\sum^{C}_{c=1} \sum^{V}_{v=1} {\beta}^v_c) = 1 $$
$$ \sum^{V}_{v=1} {\beta}^v_c \le 1,\ for\ c = 1, …, C $$
$$ \sum^{M}_{m=1} \sum^{V}_{v=1} {\beta}^v_m B^v_m + \sum^{C}_{c=1} \sum^{V}_{v=1} {\beta}^v_c B^v_c \le R \cdot L $$
$Q(\cdot)$ 是公式 1 中定义的质量; $R$ 是网络带宽; $1(x) = 1 \iff x > 0$ ;$1(x) = 0 \iff x \le 0$ ;
约束 1 强制为观看区域下载宏块或常规块的集合,只下载宏块的一个质量版本;
约束 2 规定只下载常规块的一个质量版本;
约束 3 保证视频数据可以在开始播放之前被完全下载;
给出用户的观看区域之后,候选的宏块或对应的常规块集合也可以求出。
将QoE最大化的问题分解成两个子问题:
- 确定宏块的质量等级;
- 确定常规块的质量等级;
最后的解取这两种方案能取得更大QoE的那种。
如果QoE模型不考虑常规块之间的质量差异,则整体的QoE等价于下载的常规块的平均质量等级。
确定常规块质量等级的问题则可以简化为:
$$ max\ \sum_{c \in C} \sum^{V}_{v=1} Q({\beta}^v_c v) $$
需要满足以下 2 个约束:
$$ \sum^{V}_{v=1} {\beta}^v_c = 1,\ for\ c \in C $$
$$ \sum_{c \in C} \sum^{V}_{v=1} {\beta}^v_c B^v_c \le R \cdot L $$
$C$ 表示覆盖观看区域的常规块集合。
简化之后的子问题可以通过对多项选择背包问题的简化,证明为是NP-hard问题,基于此提出启发式算法。
基于宏块的流行性感知推流
基于观看区域确定宏块
不同用户对相同视频的观看有着相似的 ROI,其视野中心是相近的,因此首先确定其视野中心并聚类到一起。
不能直接应用的知名聚类算法:
- 需要事先确定簇(即宏块)数量的算法(事先并不能确定需要多少宏块):
K-means - 簇会越聚越大的算法(这样会失去节约带宽的优点):
DBSCAN
提出的算法用 2 个参数 $\lambda$ 和 $\gamma$ 来保证彼此相近的两个视野中心被归入同一簇,同时基于簇的宏块不至于太大。
- 被归入同一簇的视野中心之间的距离应该小于等于 $\lambda$;
- 同一个簇的任意两个视野中心之间的距离应该小于等于 $\gamma$;
为了确定这两个参数,还需要考虑常规块的大小带来的影响。
算法描述:
给出用 $P$ 表示的点集,其中每个点表示一个用户的视野中心位置;
用 $N_p = \lbrace q | q \in P \land q \neq p \land dist(p, q) \le \lambda \rbrace$ 来表示与点 $p$ 之间欧式距离小于 $\lambda$ 的点集(即为临近点集);
- 初始化拥有最多临近点的点所在的簇,例如: $p = {argmax}_{p \in P} |N_p|$;
- 添加临近簇内任何点的点到簇中,扩张过程直到找不到符合条件的点位置;
- 检查簇中任意两个点之间的距离是否大于 $\gamma$ ,如果存在这种情况就使用
K-means算法将这个簇分成两个子簇; - 从 $P$ 中移除簇中的点;
- 重复 1-4 的过程直到 $P = \empty$;
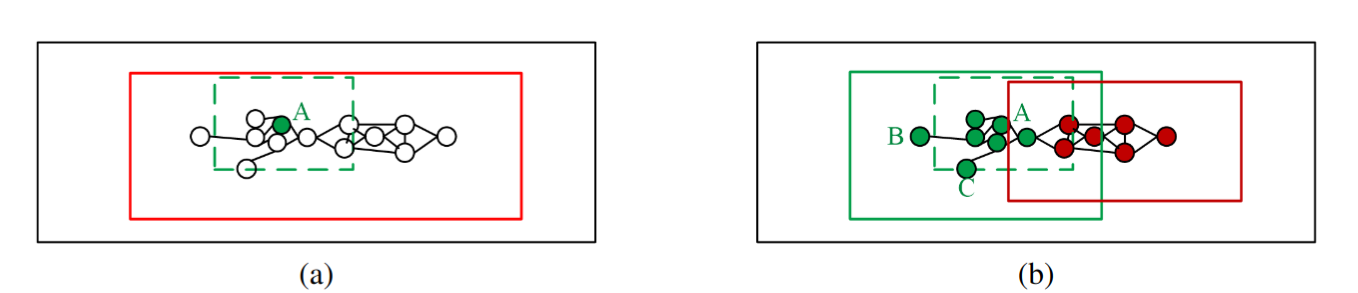
宏块优化
通过简单地覆盖簇中用户的所有观看区域来为每个簇建构宏块可能会导致建构出不必要的大宏块,因此需要确定恰当的宏块大小。
首先需要确定哪些用户的观看区域应该被用于构建宏块,这样用户下载宏块时的带宽使用率小于下载一组常规块时的带宽使用率:$B_m$ 和 $B_c$ 分别表示覆盖相同观看区域的宏块和常规块的数据量大小。
为了解决用户头部运动的随机性,宏块应该在覆盖用户观看区域之外加上一些边界区域。边界区域可以基于用户观看中心的变化来确定,变化通过在推流观看过程中以固定采样率记录。
一个视频片段中 $x(y)$ 坐标的变化定义为 $x(y)$ 坐标的标准差。
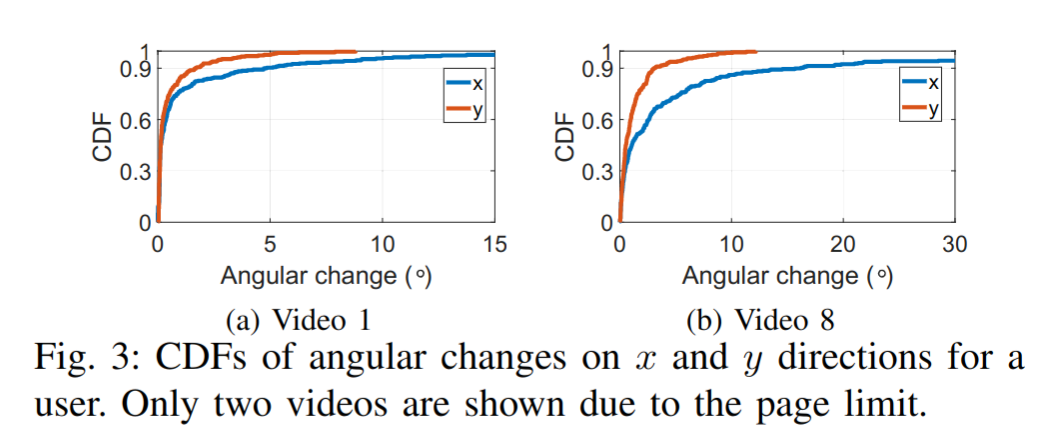
实验发现:在一个视频片段中,用户的 $x(y)$ 坐标的变化很小。
分别用 $A_x$ 和 $A_y$ 表示 $x$ 和 $y$ 方向上的变化,构建的宏块应该覆盖用户的观看区域,并为 $x(y)$ 方向加上 $\frac{A_x}{2}(\frac{A_y}{2})$ 的边缘区域。
宏块构造问题的形式化:
为每个用户 $i$ 引入二元变量 ${\alpha}_i$ ,${\alpha}_i = 1$ 表示此用户的观看区域用于构建宏块,反之则没有;
实际应用中即为:如果 ${\alpha}_i = 1$ ,则用户 $i$ 可以下载宏块;否则用户只能下载对应的常规块集合。
问题的目标是:在下载宏块或相同质量等级的常规块集合时,最小化所有用户的总带宽使用量。
$$ \underset{\lbrace {\alpha}_i \rbrace}{min}\ \sum^{N_j}_{i=1} {\alpha}_i B_m + (1-{\alpha}_i) B_c $$
$N_j$ 表示在 $j^{th}$ 簇中的用户数量;解决问题之后,可以用所有 ${\alpha}_i = 1$ 的用户观看区域构建宏块;
尽管暴力枚举法可以完成最优求解,但是其时间复杂度为 $O(2^{N_j})$ ,为了减少实际建构宏块的时间,提出一种类似于随机采样一致性算法的迭代算法,每次迭代中,所做工作如下:
- 随机选取用户观察区域的子集。
- 编码宏块,用 $B_m$ 表示构建的宏块的带宽使用量。
- 检查建构的宏块是否覆盖用户 $i \in \lbrace 1, …N_j \rbrace$ ,是则${\alpha}_i = 1$;否则 ${\alpha}_i = 0$。
- 检查总共的带宽使用量是否比之前迭代的更小,是则用当前迭代建构的宏块更新最终的宏块;否则继续迭代。
为了避免预测失败时用户看到空白区域,在下载观看区域的高质量宏块或常规块集合之外,也以最低质量下载其余的常规块。
流行性感知推流
服务端基于多个用户的历史观看信息建构宏块,同时也使用常规块的划分方案编码视频。
客户端在推流过程中选择恰当块(宏块或常规块集)的恰当的质量等级来最大化用户的QoE。
流行性感知的推流算法首先为每个视频段预测用户的观看区域,之后预取相应的宏块或常规块集。
- 使用岭回归做 VP,输入用户在一系列历史帧中的观看区域中心坐标,输出未来帧中用户的观看区域位置。
- 基于预测的观看区域,算法确定是否存在覆盖预测区域及其边缘区域的宏块,是则搜索并下载满足条件的最高质量的宏块;否则下载相应区域的常规块集。

选择常规块集时首先为所有要选择的块确定满足贷款限制的最高质量等级,分配完之后如果还有剩余的带宽,算法会根据常规块与视野中心距离的远近程度提高一个质量等级,越近越优先提高。同时考虑到空间质量差异会降低QoE,所以提高质量的行为只有在超过半数的常规块满足条件时才会执行。