论文概况
Link:TBRA: Tiling and Bitrate Adaptation for Mobile 360-Degree Video Streaming
Level:ACM MM 21
Keywords:Adaptive tiling and bitrate,Mobile streaming
创新点
背景
现有的固定的 tile 划分方式严重依赖 viewport 预测的精度,然而 viewport 预测的准确率往往变化极大,这导致基于 tile 的策略实际效果并不一定能实现其设计初衷:保证 QoE 的同时减少带宽浪费。
考虑同样的 viewport 预测结果与不同的 tile 划分方式组合的结果:
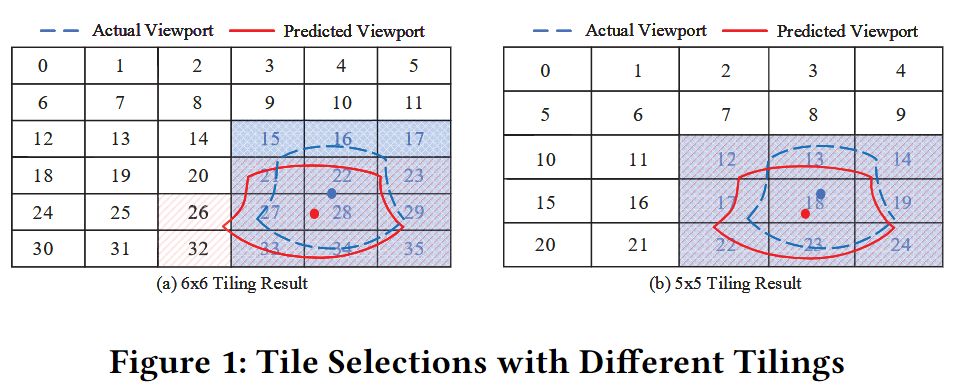
从上图可以看到:
- 如果采用$6 \times 6$的分块方式,就会浪费 26,32 两个 tile 的带宽,同时 15,16,17 作为本应在实际 viewport 中的 tile 并没有分配最高的优先级去请求。
- 如果采用$5 \times 5$的分块方式,即使预测的结果与实际的 viewport 有所出入,但是得益于 tile 分块较大,所有应该被请求的 tile 都得到了最高的优先级,用户的 QoE 得到了保证。
另一方面,基于 tile 的方式带来了额外的编解码开销(可以看这一篇论文:note-for-optile),而这样的性能需求对于移动设备而言是不可忽略的。
创新
除了考虑常见的因素如带宽波动和缓冲区占用之外,提出同时自适应分块策略和码率分配以应对变化的 viewport 预测性能和受限的移动设备的解码能力。
论文组织
- 首先使用现实世界的轨迹分析了典型的 viewport 预测算法并确定了其性能的不确定性。
- 接着讨论了不同的分块策略在 tile 选择和解码效率上的影响。
- 自适应的分块策略可以适应 viewport 预测的错误,并能保证 tile 选择的质量。
- 为解码时间建构了分析模型,可以在给定受限的计算资源时用于选择恰当的分块策略和码率。
- 形式化了优化模型,讨论了自适应算法的细节。
- 评估证明了方案的优越性。
Motivation
分块策略对 tile 选择的影响
实现 4 种轻量的 viewport 预测算法:线性回归 LR、岭回归 RR、支持向量回归、长短期记忆 LSTM。
设置历史窗口大小为 2s,预测窗口大小为 1s;viewport 的宽度和高度分别为 100°和 90°。
默认的分块策略为$6 \times 6$;头部移动数据集来自公开数据集。
viewport 预测的不准确性
研究表明,用户的头部运动主要发生在水平方向而较少发生在垂直方向,所以只分析水平方向的预测。
实际的商业移动终端只有有限的传感和处理能力,并不能支持高频的 viewport 预测采样。
视频内容的不同类型会显著影响预测的精度,基于录像环境(室内或户外)和相机的运动状态分类。
改变采样频率会直接影响 viewport 预测的精度,频率越低,精度越低。
相机运动的 viewport 预测错误率比相机静止的明显更高。
通过分块容忍预测错误
因为不管 tile 的哪个部分被包含在预测的 viewport 中,只要包含一部分就会请求整个 tile,所以增大每个 tile 的尺寸能吸收预测错误。
实验验证:
设定从$4 \times 4$到$10 \times 10$的分块方式,使用不同的预测误差来检查分块设定可以容纳的最大预测误差,同时保持 tile 选择结果的相同质量。
用$F_1$分数来表示 tile 选择的质量:$F_1 = \frac{2 \cdot precision \cdot recall}{precision + recall}$。
实验结果表明更大的 tile 尺寸更能容忍预测错误。
分块策略对解码复杂性的影响
虽然当前的移动设备硬件性能发展迅速,但是实时的高码率高分辨率全景视频的解码任务还是充满挑战。
分块对于编码的影响:
- tile 越小,帧内和帧间内容的相关区域就越小,编码效率越低。
直接影响解码复杂性的因素:
- tile 的数量。
- 视频的分辨率。
- 用于解码的资源。
固定其中 1 个因素改变另外 2 个因素来检查其对解码的影响:
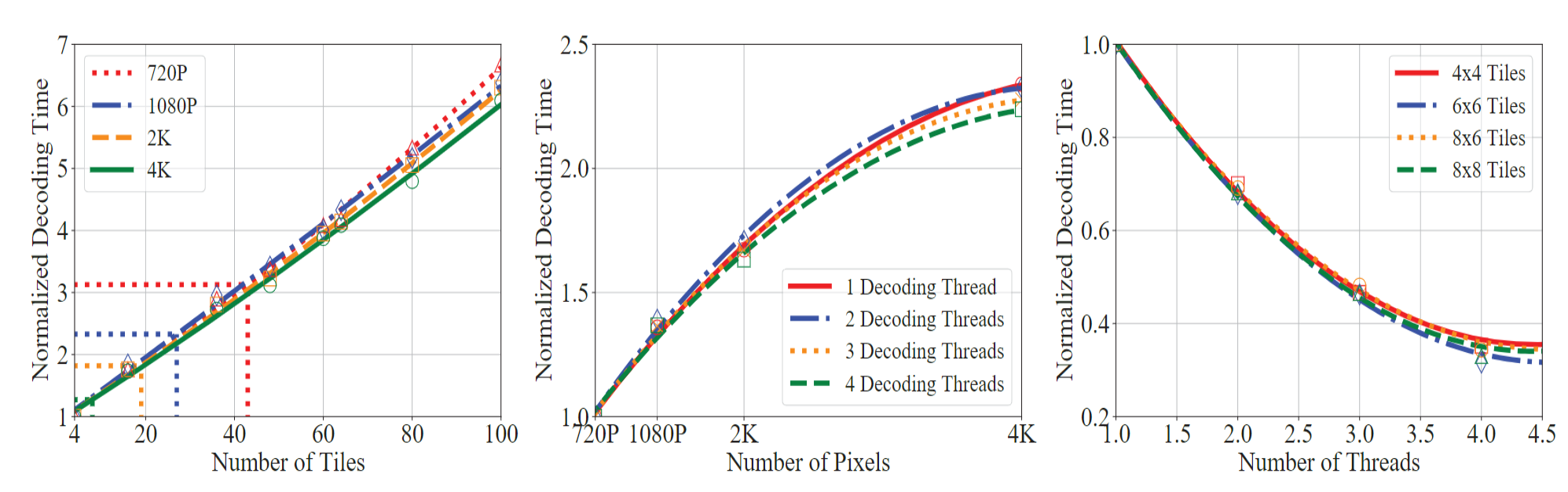
根据对图的观察可以得出这 3 个因素在经验上是相互独立的,因为这三幅图之中的图像几乎相同。
分别用$F_n(x), F_r(x), F_c(x)$表示 tile 数量、分辨率、线程数量为$x$时,解码时间与基线时间的比值。
将这 3 个比值作为 3 个乘子建立分析模型:
$$ D = D_0 \cdot F_n(x_1) \cdot F_r(x_2) \cdot F_c(x_3) $$
上式表示计算整体的解码时间,其中 tile 数量为$x_1$、分辨率为$x_2$、线程数量为$x_3$;$D_0$时解码的基线时间。
这个模型将用于帮助做出分块和码率适应的决策。
注意在实际情况中,可供使用的计算资源(线程数)是受限的,需要根据设备当前可用的计算资源来分配。
TBRA 的设计
- $S = \lbrace s_1, s_2, … \rbrace$ 表示 360°视频分块方式的集合;
- 对于分块方式$s_i$,$|s_i|$ 表示这种方案中 tile 的数量;
- 当 $i < j$ 时,假设 $|s_i| < |s_j|$;
- 对于分块方式$s$, $b_{i, j}$ 表示第 $i$ 块的 tile $j$,$i \le 块的数量, j \le |s|$;
- 目标是确定分块方式$s$,并为每个 tile 确定其码率$b_{i, j}$;
分块自适应
自适应的概念
分块尺寸大小会导致 viewport 容错率和传输效率的变化。
- 分块尺寸小,极端情况下每个像素点作为一个 tile,viewport 容错率最小,但是传输效率达到 100%;
- 分块尺寸大,极端情况下整个视频帧作为一个 tile,viewport 容错率最大,但是传输效率最小;
优化的目标就是在这两种极端条件中找到折中的最优解。
分块选择
以$\overline{r_d}, d \in \lbrace left, right, up, down \rbrace$为半径扩大预测区域;$e_d$表示过去 n 秒中方向 $d$ 的预测错误平均值;
$$ \overline{r_d} = (1-\alpha) \cdot \overline{r_d} + \alpha \cdot e_d $$
预测区域的扩展被进一步用于 tile 选择,受过去预测精度的动态影响。
下一步检查不同分块方式,进而找到 QoE 和传输效率之间的折中。
对于每个分块方式,比较基于扩展的预测区域的 tile 选择的质量。使用 2 个比值作为 QoE 和传输效率的度量:
$$ Miss\ Ratio = \frac{of\ missed\ pixels\ in\ expanded\ prediction}{of\ viewed\ pixels} $$
$$ Waste\ ratio = \frac{of\ unnecessary\ pixels\ in\ expanded\ prediction}{of\ viewed\ pixels} $$
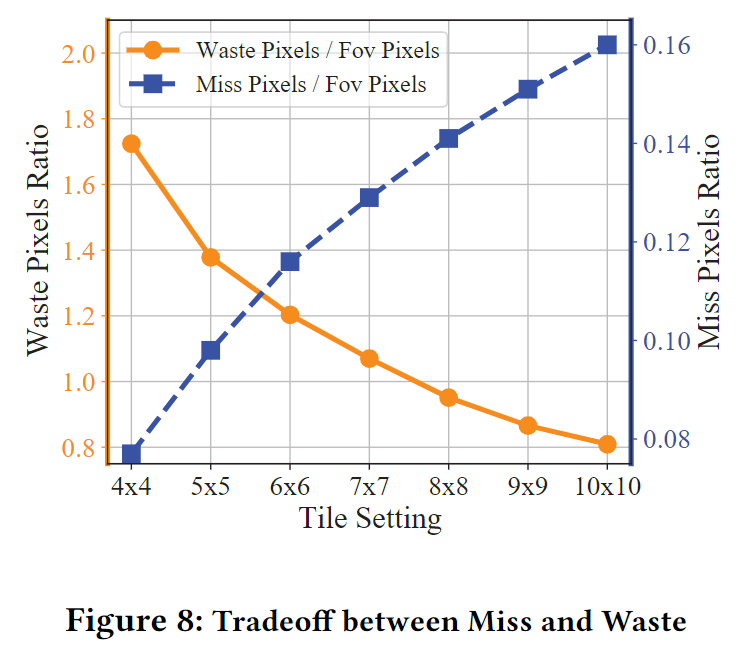
这 2 个比值的 tradeoff 可以在上图中清晰地看出。
使用分块方式对应的惩罚$Tiling\ i_{penalty}$来评估其性能:
$$ Tiling\ i_{penalty} = \beta \cdot Miss\ Ratio + |1/cos(\phi_i)| \cdot Waste\ Ratio $$
$\phi_i$ 是 viewport $i$ 的中心纬度坐标,它表明随着 viewport 的垂直移动,浪费率的权重会发生变化。(因为投影方式是 ERP)
检查完所有的方式之后,最终选择惩罚最小的分块方式。
码率自适应
视频质量
$w_{i, j}$表示在第 $i$ 个视频块播放时,tile $j$ 的权重;在当前方案中 $w_{i, j} = 0\ or\ 1$ 取决于 tile 是否在预测的 viewport 中。
$q(b_{i, j})$ 是 tile 比特率选择 $b_{i, j}$ 与用户实际感知到的质量之间的非递减映射函数。
第 $i$ 个视频块的质量等级可以定义为:
$$ Q^{(1)}_i = \sum^n_{j=1} w_{i, j} q(b_{i, j}) $$
使用最新研究的主观视频质量模型:
$$ subjective\ PSNR:\ q_i = PSNR_i \cdot [M(v_i)]^{\gamma} [R(v_i)]^{\delta} $$
$M(v_i)$ 是检测阈值;$R(v_i)$ 是视网膜滑移率;$v_i$ 是第播放 $i$ 个视频块时 viewport 的移动速度;$\gamma = 0.172, \delta = -0.267$
质量变化
连续视频块之间的强烈质量变化会损害 QoE,定义质量变化作为响铃两个视频块之间质量的变化:
$$ Q^{(2)}_i = |Q^{(1)}_1 - Q^{(1)}_{i-1}|,\ i \in [2, m] $$
重缓冲时间
参数设置:
- $C_i$ 表示下载视频块 $i$ 的预计吞吐量;
- $B_i$ 表示客户端开始下载视频块 $i$ 时缓冲区的占用率;
- $B_{default}$ 表示在启动阶段默认的缓冲区填充等级,记 $B_{default} = B_1$;
- 下载第 $i$ 个视频块需要时间 $\sum^n_{j=1} b_{i, j} / C_i$ ;
- 每个视频块的长度为 $L$ ;
缓冲区的状态应该在每次视频块被下载的时候都得到更新,则下一个视频块 $i+1$ 的缓冲区占用情况可以计算为:
$$ B_{i+1} = max\lbrace B_1 - \sum^n_{j=1} b_{i, j} / C_i,\ 0\rbrace + L $$
下载第 $i$ 个视频块时的重缓冲时间可以计算为:
$$ Q^{(3)}_i = max \lbrace \sum^n_{j=1} b_{i, j} / C_i - B_i,\ 0 \rbrace + t_{miss} $$
第一部分是下载时间过长且缓冲区耗尽,视频无法播放情况下的重新缓冲时间;
第二部分 $t_{miss}$ 表示下载缺失的 tile 所花费的时间(在视频块播放过程中被看到但是之前没有分配码率的 tile)。
优化目标
第 $i$ 个视频块的整体优化目标可以定义为前述 3 个指标的加权和:
$$ Q_i = pQ^{(1)}_i - qQ^{(2)}_i - rQ^{(3)}_i $$
各个系数的符号分配表示:最大化视频质量、最小化块间质量变化、最小化重缓冲时间。
传统意义上使用所有视频块的平均 QoE 作为优化对象,但实际上很难获得从块 $1$ 到块 $m$ 的整个视界的完美的未来信息。
为了处理预测长期吞吐量和用户行为的难度,采用基于 MPC 的框架,在有限的范围内优化多个视频块的 QoE,最终的目标函数可以形式化为:
$$ \underset{b_{i, j}, i \in [t, t+k-1], j \in [1, n]}{max} \sum^{t+k-1}_{i=t} Q_i $$
因为短期内的 viewport 预测性能和网络状况可以很容易得到,QoE 优化可以通过使用窗口 $[t, t+k-1]$ 内的预测信息;
接着将视界向前移动到 $[t+1, t+k]$ ,更新新的优化窗口的信息,为下一个视频块执行 QoE 优化,直到最后一个窗口。
使用基于 MPC 的公式的优点:由于受限的问题规模,每个优化问题的实例都是实际可解的。
高效求解
提出的公式天然适合在线求解,得益于短窗口的实例问题规模很小,QoE 优化可以通过详尽搜索定期解决。
但是因为优化过程需要高频调用,所以对于大的搜索空间还是充满挑战。
为了支持实时优化,需要对搜索空间进行高效剪枝,确定几点约束:
解码时间需要被约束;
解码时间应该短于回放长度。
给定移动设备上可用的计算资源,可以得到支持的最大解码线程数。
基于解码时间的分析模型,由于解码复杂度和分辨率的单调性,可以找到设备能够限定时间内解码的最大质量水平,这会将码率选择限制在有界搜索空间内。
码率选择应该考虑吞吐量的限制:$\sum^n_{j=1} b_{i, j} \le LC_i$ ;
不会主动耗尽缓冲区,无需让其处理吞吐量的波动。
码率选择应该考虑 tile 的分类;
tile 的码率不应该低于同一个视频块中更低权重 tile 的码率: $b_{i, j} \ge b_{i, j’}, \forall w_{i, j} > w_{i, j’}$ 。
属于相同类别的 tile 比特率选择应该是同一个等级;
这使码率自适应在 tile 类的级别上执行而非单个 tile 的级别,大大减小了搜索空间的规模。
当优化窗口中的吞吐量和用户行为保持稳定时,同一个窗口中的 tile 应该有相同的结果。
TBRA workflow

这样的方式需要在服务端存储大量的按照不同分块方式划分的不同码率版本的视频块,这一点可以进一步研究。
但是对于移动终端设备而言,这样的解决方案只引入了可以忽略不计的开销。
观察到 tile 自适应问题具有全局最优通常就是局部最优的特点,因此可以大大减少计算量。
基于 MPC 的优化 workflow 还可以有效地解决码率自适应问题。